Blog Reflection

Throughout this course I think I have engaged a lot with various methodologies that are radically different than the traditional curriculum (using art in the Math art project, integrating social justice in Stocker, environmental studies our visit to the orchard garden) but that are not a result of my own interests and my own research. It felt a bit like these topics were being forced on me, and that they don't align with how I would bring about non-traditional elements in the classroom. I imagine it would have been a lot nicer to have less focus EXCLUSIVELY on non-traditional ways of teaching mathematics, but rather have that as a SINGLE, OPEN-ENDED opportunity to bring in one's own interests in multi-disciplinary fields and to critically reflect on how these things ought to be integrated in the mathematics class-room. Instead, this topic took over the entire course and left very little room for us to actually develop and practice our OWN pedagogies and teaching styles. I also found that our investigation into the curriculum and textbooks was shallow at best, and there was not exposure on how one goes about using the curriculum to design lessons. Instead, those things we had to teach ourselves and we were taught in class how to "look" at a textbook. The course lacked any exercises that could bring about true growth as a mathematics teacher. It was an incredibly narrow scope and I honestly learned more about mathematics teaching in my inquiry class than this one (even though my inquiry class is not SUPPOSED to be exclusively for math....).

Math (Un)fair

I like the open ended nature of the project: make any kind of statistical probability game but it might be fair or unfair. I think the students came to understand the concepts very well but it was quite repetitious. I did also like the idea of collecting data that illustrates how statistics work. I imagine that could help the students connect theory and experiment, a very important concept. I don't have much else to comment, I think it was well executed.

Unit Plan

Here is the link to my unit plan for the course.

https://docs.google.com/document/d/1okzo2F05YYugtBGcc5csaGWjxXGv-lJJMR_nE3jd_JE/edit?usp=sharing

Stocker

I acknowledge that today in my young adulthood I have more skills and confidence than I even know how to deal with and use efficiently, but a lot of this cultural and intellectual capital was not granted to me at birth and a lot of the knowledge that I use now is due to my interest and engagement with the world in a mathematical way. My aim as a secondary teacher is to teach mathematics as a means of acquiring autonomy, and to give my students access to a wider perception of the world as to make choices that will bring them to places of power and comfort based on their individual needs and wants. In particular, to use that power to challenge and question the world and it's social structures with logical justifications, ideally as a means of making it more equitable. Of course, each student is encouraged to use their aptitudes, passions, and energy in any way that they see will be an addition to their livelihood.
I imagine this textbook is an attempt at providing curricular resources for a hopeful emerging of the popular idea that mathematics, along with all other subjects at school, should be used as a means of empowering students to engage with the social structures around them and think critically about how to live in the world. I agree with a lot of the points raised in the introduction and of particular note the choice to use a quote from "Nel Noddings", quite possibly the Nel who questions the use of everything, at the beginning of the chapter;
 

I think there are clear relationships between logic, philosophy, sociology, and mathematics. These connections pose questions like why things work, how do we fix things, and where should I start? Questions of this sort are relative and each individual encounters different problems and challenges in the real world and engages with them relative to each of these unique experiences. The questions are common no matter how different the experiences, and thus providing opportunities for students' minds to reflect and think critically about the world in these ways is extremely important in the goal of "producing" intelligent and creative children. I imagine mathematics as a discipline that tries to model the world in a systematic way through defining rules from playing off of physical intuition and logic. When a student is doing mathematics the goal should be that they come to see the pieces in that model, why they work, and how it can perhaps be done "better" or more "efficiently" (and why it is important to define these parameters in a systematic or arbitrary way).

This textbook seems to provide concrete ways in which teachers teach concepts of social justice in their classrooms. I think it is certainly interesting to explore lessons of this sort, and it is becoming more welcome with the emergence of the new curriculum. I look forward to promoting my students to use their knowledge and skills to shake things up and make the world more fun.

Math Art Project Reflections

In the math art project myself, Jing, and Devon all had distinct and independent interpretations in how we can deconstruct interesting 3D objects into a set of simpler 2D constructions. I really enjoyed collaborating and discussing on how we can in-cooperate all of these unique perspectives and come full circle to illustrate how different kinds of art and structure can be creating through have a conceptual understanding of mathematics.

I personally decided to use my skills in programming, specifically Scientific Computing, to break up two shapes into a finite number of 2D cross-sections as a means of creating a blue-print for a sculpture. The sculpture I chose was a hyperboloid of one sheet (above: an image I generated of this surface using Matlab) inside of a sphere. Sadly, the glue I used was not strong enough (Rest In Pieces hyperboloid sphere) but I was able to perfectly construct the figure I had in mind. In our activity we illustrated that by going through a range for a specific variable, the choice of that variable being important based on the geometry of the surface, one can make physical sculptures of 3D mathematical surfaces defined using algebraic expressions. I think the use of art as an application for having a conceptual understanding of mathematics is interesting and can certainly be seen in the physical word with incredible works of engineering and design surrounding us. Art is more accessible than math as it generally is open-ended and doesn't require strict rules and generally is aided from a bit of chaos and creativity, but incorporating technical components into art can allow for very interesting pieces that are still equally prone to the chaos and creativity of art as it is very easy to make a single mistake and build off of it to make something unique and beautiful.

Micro-teaching feedback

Access to lesson plan: https://docs.google.com/document/d/1BorOSa41kvwdXHcyt5VCKaUzoGO8V8fJEW8xbw0sw2M/edit?usp=sharing

In this team-teaching I think Erika and I did a relatively good job trying to present something that seems technical and boring in a fun and interesting way. The activity related the representation of areas with unknown distances with the multiplication of binomials, ultimately allowing the student to understand the expression geometrically. We then did the algebraic explanation and looked at some applications when employing this formula and how there are different circumstances when we might use different of squares in order to change the expression such that the two terms are squared (i.e rationalizing the denominator using the conjugate).

After reflecting I don't think I would have done much differently. The activity went on a little bit longer than intended, but that was because we anticipated the students making the connections faster. Instead we took more time to ensure that everyone finished the activity and worked one on one with the students to guide and facilitate the completion of the proof. I think we rightly decided that the students would get more out of the lesson with a focus on the interactive aspect of the lesson. If this was my actual class, it would not be such a big deal that we did not cover every single detail that we had hoped to, and there would be an opportunity to review and bring it back to the big idea in the proceeding classes. It was a good experience to do the micro-teaching, and it solidifies my confidence and enthusiasm for teaching mathematics.

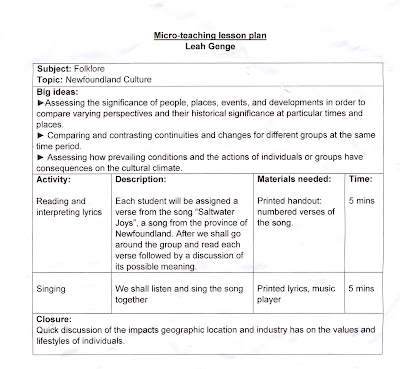
Micro teaching

I am really pleased everyone seemed to enjoy the activity. If I could re-do the lesson I would print out full lyrics for everyone and play the song itself. Thank you again friends for sharing some stuff about my home :)

Battleground Schools

This article is based primary on two categorizations of mathematics; the progressive and the conservative. Of particular note, the progressive stance was said to use mathematics as a method for posing questions as opposed to a method for answering them in a more conservative stand point. When the difference between these two stances on mathematics education was made I found it interesting that in more conservative methods there was mention of a focus on remaining in control of students and how perhaps this focus on using math as a mechanism to force compliance is one of the reasons people feel disdain toward the subject. For this reason, the article seems to show clear bias for a more progressive stance in mathematics education.

This is also illustrated further in the article with mention of religious and traditionalist groups valuing this more authoritarian view of mathematics. It is certainly interesting that people have a tendency to lean toward one stance on mathematics education based on their political views. Certainly we should hope curriculum and schools are non-secular and make an effort to remain neutral to any particular political movements, even the progressive ones. I think there is still a lot of work to be done to bring about critical thinking in students and let them make political decisions and affiliations for themselves. In mathematics education, in any case, more autonomy is being given to the teacher to use different mechanisms for teaching a very technical but also abstract subject.

Just as these standards have been doubted by many, I imagine the new BC curriculum might also have a bit of a difficult time becoming the standard. In any case, it seems to be a step in the right direction.

       vs     

Eisner

I think Eisner's analysis of the implicit and null curriculum outline a lot of changes that ought to be made in one's conceptualization and implementation of curriculum.

Implicit: In the first half of the paper Eisner illustrated the implicit consequences of schooling and how in a lot of ways these, as they are now, can harm childrens' ability to learn. In particular he spends a great deal of time talking about how we teach compliance instead of critical thinking and how this is connected to the values of structured schooling such as in well-known universities and other post-secondary institutions. As these sorts of institutions are dis-proportionally accessible to higher classes and give explicit merit in black and white intellectual capital this reflects schools' roll in systemically privileging people whom are already privileged. Something like a public school system should be designed as to help all students grow and learn such that they can use their competencies to engage with life and meet it's challenges.

One interesting thing that stood out to me was Eisner's use of sociological criticisms of technology as a metaphor with schooling. He also mentions how the arts are undervalued and efficiency and economy are the core values behind the design of current schools. In a society where technology is rapidly changing how we access content and how much labour is needed as we reach further automation there needs to be a shift in how we wish to use human capital. Soon we will reach a time where not all humans will need to work, or at the very least the work force will look very different, and for that reason Eisner argues that there needs to be a change in what we teach both explicitly and implicitly.

Null: This section discusses the consequences of neglecting to teach certain things within schools. In particular, the rigorous scheduling requirements for "core subjects" such as the Sciences and Language. When schooling is overly prescriptive then the implicit values of economy and efficiency compromise place for other values, such as art.

The new BC curriculum's aim appears to be to adopt similar ideals, looking to replace the intrinsic curriculum with inquiry and critical thinking and also trying to bring in multi-dimensional teaching settings in an effort to incorporate the arts within traditional subject matter. I think that some of the critiques raised by Eisner, such as precise scheduling, rewarding and expecting complacency, existence of extrinsic awards, among others, could be better addressed with further adjustments to this inquiry based curriculum.

TPI

Unsurprisingly my TPI states that I lean toward the values of social reform and fostering a nurturing educational setting. I also seem to value the development over the transfer of knowledge and taking students as apprentices.

These results are no surprise to me. I chose to become a teacher mainly because I think a lot of the public institutions are made such that the same people are systematically marginalized and then blamed for their inability to contribute. I am very lucky to have intellectual capital and a support system that allowed me to reach this level of success, but not everyone in the same situation. I hope to level the playing field in my own microscopic way by providing all student a support system and encouraging critical thinking and thoughtful rebellion.

My Mathematical Past

Skemp and relational understanding

In order to have deep understanding of mathematics it must be seen as a language as opposed to a set of rule and operations. Language is created by assigning a symbol to an abstract concept. We traditionally understand these to be words and grammar but in the context of mathematics it becomes notation. In Skemp's article they rightfully point out that many students have the ability to perform operations and memorize notation, but often times the effects of this are short-term and do not bring about progression and retention. Students often times do not actually have a clear idea about what the abstract concepts that are being represented by notation and thus can perform very well in the setting of examinations but not when being asked to think and build on material that has already been taught.


In the article there was an interesting discussion on the difficulties in changing the focus in math education on a true meaning of understanding- what they call "relational understanding"- due to the advantages of "instrumental understanding".  One of the advantages of instrumental learning that was mentioned was the evaluation schemes in the status quo for math. In my opinion it is not adequate to exclusively test a student's ability to perform rules and operations. There must be a way to equally evaluate the actual relational understanding of the subject, and the article presents a very good example with units in relation to area. Evaluations ought be thought-provoking and help students discover the nuances of the abstractions we define using notation. The article also pointed out different approaches one can take in introducing theoretical concepts and having the importance of that inclusion be known. Abstract concepts are difficult for everyone to understand, but especially children. The article's focus on accessible ways of relating abstract math with concrete math is a good first step toward bringing about the necessary components of mathematics that bring about true deep understanding in students.